ΟΙ ΠΕΝΤΕ ΕΞΙΣΩΣΕΙΣ ΠΟΥ ΑΛΛΑΞΑΝ ΤΟΝ ΚΟΣΜΟ

Συνεχώς αποδεικνύεται ότι μόνο μια απλή φόρμουλα χρειάζεται για να ξεκλειδώσει κανείς τα μεγάλα μυστικά του σύμπαντος. Χωρίς τις εξισώσεις ο κόσμος δεν θα είχε την μορφή που γνωρίζουμε σήμερα. Ο κόσμος αλλάζει και καθορίζεται ξανά και ξανά από τις εξισώσεις. Πάμε να δούμε τις πέντε εξισώσεις που άλλαξαν τον κόσμο.

ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ

Το τετράγωνο της υποτείνουσας ενός ορθογωνίου τριγώνου ισούται με το άθροισμα των τετραγώνων των δυο κάθετων πλευρών. Την πρόταση αυτή την παρέχει ο Ευκλείδης στο βιβλίο των Στοιχείων Γεωμετρίας με απόδειξη από τον Πυθαγόρα. Το θεώρημα αυτό έχει ίσως τον μεγαλύτερο αριθμό αποδείξεων από κάθε άλλο μαθηματικό θεώρημα. Η δύναμη του βρίσκεται στην απλότητα του. Κάποιες από τις συνέπειες και τις χρήσεις του είναι οι Πυθαγόρειες τριάδες, τα μη μετρήσιμα μεγέθη, δηλαδή ευθύγραμμα τμήματα τα μήκη των οποίων είναι μη μετρήσιμα (ρίζες) μπορούν να κατασκευαστούν με χάρακα και διαβήτη, η ευκλείδεια απόσταση σε διάφορα συστήματα συντεταγμένων, όπως το καρτεσιανό, η πυθαγόρεια τριγωνομετρική ταυτότητα που μας λέει πως ημ^2(θ)+συν^2(θ)=1   και πολλές πολλές ακόμα.

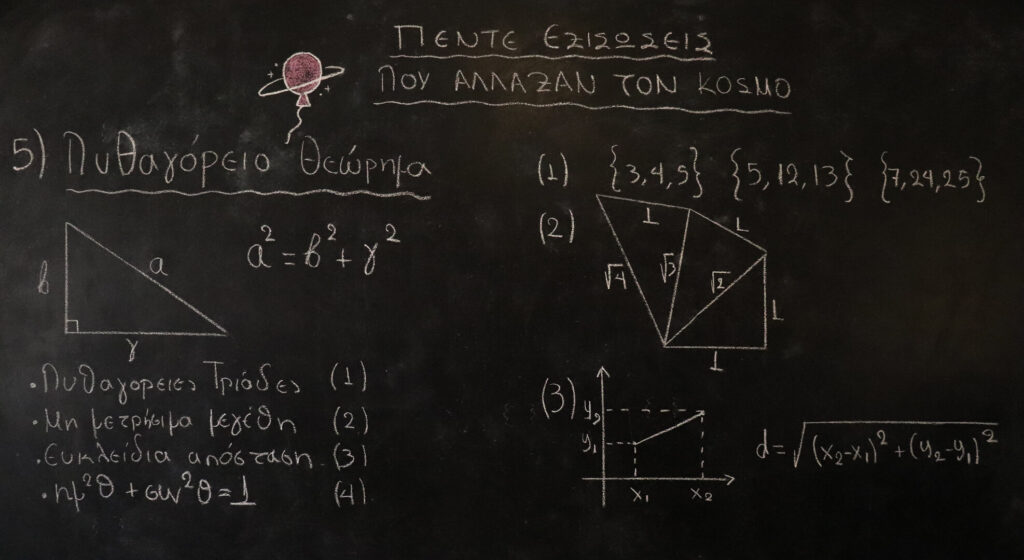
ΛΟΓΑΡΙΘΜΟΙ

Οι λογάριθμοι εισήχθησαν από τον σκοτσέζο μαθηματικό, φυσικό και αστρονόμο John Napier στης αρχές του 17^ου αιώνα. Στην σημερινή εικόνα των λογαρίθμων καθοριστικό ρόλο έπαιξε και ο Leonard Eueler, ο οποίος τους συνέδεσε με την εκθετική συνάρτηση. Οι λογαριθμικές κλίμακες περιορίζουν το πεδίο τιμών ποσοτήτων σε μεγάλο εύρος, για παράδειγμα το ντεσιμπέλ και το pH είναι λογαριθμικές μονάδες μέτρησης. Οι λογάριθμοι έχουν πολλές εφαρμογές εντός και εκτός μαθηματικών. Χαρακτηριστικό παράδειγμα εικόνας είναι το όστρακο ναυτίλος, όπου κάθε τμήμα του οστράκου είναι αντίγραφο του επόμενου κλιμακούμενο κατά ένα σταθερό παράγοντα. Οι λογαριθμικές κλίμακες είναι φοβερά χρήσιμες για την ποσοτικοποίηση των σχετικών αλλαγών μιας τιμής. Η μεγάλη χρησιμότητα αυτού είναι η συμπίεση μιας μεγάλης κλίμακας επιστημονικών δεδομένων επειδή η λογαριθμική συνάρτηση log(x) αυξάνεται πολύ αργά για μεγάλα χ.

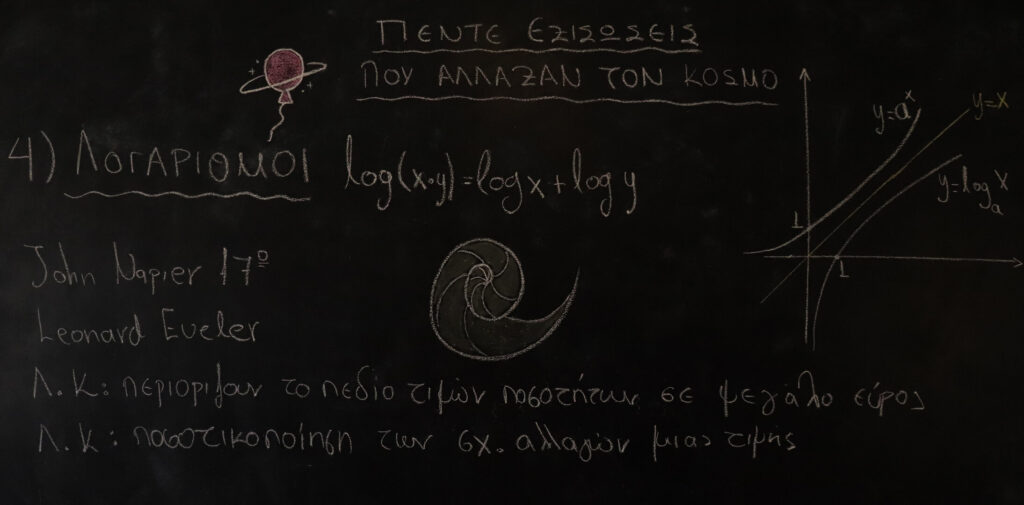
ΝΟΜΟΣ ΤΗΣ ΠΑΓΚΟΣΜΙΑΣ ΕΛΞΗΣ

Οι ελκτικές δυνάμεις μεταξύ δυο ουράνιων σωμάτων είναι ανάλογες του γινομένου των μαζών τους και αντιστρόφως ανάλογες του τετραγώνου της μεταξύ των κεντρών μαζών τους απόστασης. Ο νόμος που όρισε ο Isaac Newton έδωσε εξήγηση στους νόμους που είχε θέσει προηγουμένως ο Kepler με πρώτον αυτόν που έκανε λόγο για την ελλειπτική τροχιά των πλανητών γύρω από τον Ήλιο. Εξαιτίας του νόμου αυτού και όχι φυσικά αδίκως ο Newton θεωρήθηκε πατέρας της ουράνιας μηχανικής καθώς έπαιξε καθοριστικό ρόλο στην επεξήγηση της εξέλιξης του σύμπαντος. Η χρήση βέβαια του Νόμου της Παγκόσμιας Έλξης για την εξήγηση κοσμολογικών φαινομένων αντικαταστάθηκε από την γενική θεωρία της σχετικότητας του Einstein η οποία περιγράφει την βαρυτική δύναμη μέσω των καμπυλώσεων του χωροχρόνου παρουσία μάζας.

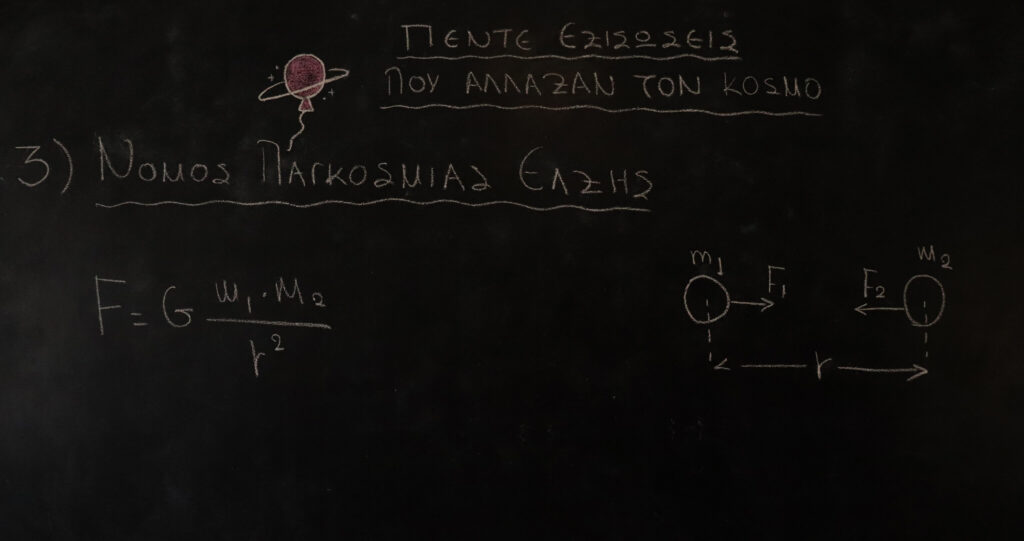
ΘΕΩΡΙΑ ΤΗΣ ΣΧΕΤΙΚΟΤΗΤΑΣ

Το 1905 ο Albert Einstein δημοσιεύει την ειδική θεωρία της σχετικότητας και προτείνει έτσι δραστικές αναθεωρήσεις των κλασσικών εννοιών του χώρου και του χρόνου. Τα δυο απλά αξιώματα στα οποία βασίζεται η θεωρία της σχετικότητας είναι:

1. Οι νόμοι της φυσικής είναι ίδιοι σε όλα τα αδρανειακά συστήματα αναφοράς και
2. Η ταχύτητα του φωτός είναι ίδια σε όλα τα αδρανειακά συστήματα αναφοράς.

Ας δούμε τώρα πως τα αξιώματα αυτά επηρεάζουν την έννοια του χρόνου.

Όσον αφορά τον χρόνο να αναφερθούμε αρχικά στην έννοια του ταυτοχρονισμού. Η έννοια αυτή υπεισέρχεστε σε κάθε μέτρηση χρονικής στιγμής. Όταν λέμε π.χ ότι έφαγα στις 2 η ώρα, εννοούμε ότι τα δύο γεγονότα (έφαγα, 2 η ώρα) έγιναν ταυτόχρονα. Το θέμα όμως είναι πως τα δύο γεγονότα αυτά που είναι ταυτόχρονα για ένα σύστημα αναφοράς δεν είναι ταυτόχρονα για ένα άλλο σύστημα το οποίο κινείται ως προς το πρώτο. Για την σχετικότητα του χρόνου υπάρχει η σχέση που εμφανίζετε στον πίνακα

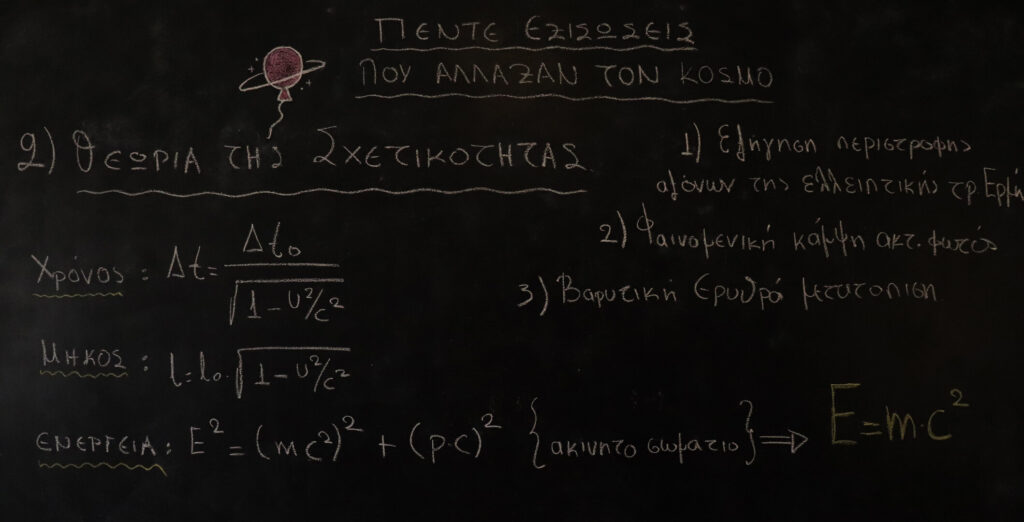
Όπου Δto  είναι η χρονική διάρκεια δυο γεγονότων που συμβαίνουν σε ένα σύστημα αναφοράς που ο παρατηρητής ηρεμεί και Δt είναι η χρονική διάρκεια που μετράει ένας παρατηρητής σε ένα κινούμενο σύστημα αναφοράς ως προς το πρώτο ευθύγραμμα με ταχύτητα u. Τότε παρατηρούμε πως ο παρονομαστής εφόσον είναι πάντα μικρότερος της μονάδος το Δt θα είναι μεγαλύτερο από το Δto. Το φαινόμενο αυτό είναι η διαστολή του χρόνου.

Με παρόμοιο τρόπο μπορούμε να δούμε πως επηρεάζεται το μήκος και η ενέργεια.

Η γενική θεωρία της σχετικότητας έχει επαληθευτεί πειραματικά σε αρκετές περιπτώσεις μερικές εκ των οποίων είναι :

• Η εξήγηση της περιστροφής των αξόνων της ελλειπτικής τροχιάς του πλανήτη Ερμή που είναι γνωστή ως μετατόπιση του περιηλίου
• Η φαινομενική κάμψη των ακτινών φωτός μακρινών αστέρων όταν περνούν κοντά από τον ήλιο και
• Η βαρυτική ερυθρά μετατόπιση, δηλαδή η αύξηση του μήκους κύματος του φωτός που  εκπέμπεται από μια πηγή μεγάλης μάζας.

ΕΞΙΣΩΣΕΙΣ MAXWELL

Ο Maxwell διατύπωσε μια σειρά εξισώσεων ο οποίες ένωσαν εξισώσεις ηλεκτρισμού, μαγνητισμού και οπτικής. Οι εξισώσεις του πέτυχαν μια από της σημαντικότερες ενοποιήσεις στον χώρο της φυσικής. Έχουμε δει πως το ηλεκτρικό και το μαγνητικό πεδίο που είναι υπεύθυνα για την ηλεκτρική και μαγνητική δύναμη είναι άμεσα συνδεδεμένα.

Η διαφορική μορφή της πρώτης εξίσωσης συνδέει το ηλεκτρικό πεδίο με την κατανομή του φορτίου στον χώρο. Μας δείχνει δηλαδή το πως τα ηλεκτρικά φορτία είναι οι πηγές του ηλεκτρικού πεδίου.                                                                                                                                                

Η μορφή της δεύτερης εξίσωσης μας δείχνει πως η μαγνητική ροή που διέρχεται μέσα από μια κλειστή επιφάνεια είναι μηδέν.

Η διαφορική μορφή της εξίσωσης αυτής μας δείχνει πως ένα μεταβαλλόμενο μαγνητικό πεδίο δημιουργεί ένα μεταβαλλόμενο ηλεκτρικό πεδίο.

Η διαφορική μορφή της τελευταίας εξίσωσης μας δείχνει πως στο μαγνητικό πεδίο συνεισφέρει και ένα μεταβαλλόμενο ηλεκτρικό πεδίο. Δηλαδή το μεταβαλλόμενο ηλεκτρικό πεδίο δημιουργεί ένα μεταβαλλόμενο μαγνητικό πεδίο. Και το μεταβαλλόμενο μαγνητικό πεδίο δημιουργεί ένα μεταβαλλόμενο ηλεκτρικό πεδίο κ.ο.κ.  

Η λίστα φυσικά των εξισώσεων που άλλαξαν των κόσμο δεν είναι ούτε στο ελάχιστο τόσο μικρή. Άλλες λίγο, άλλες πολύ μα η κάθε μια έδωσε απάντηση σε κάποιο ερώτημα συνθέτοντας έτσι το puzzle της κατανόησης του σύμπαντος.