ΠΕΙΡΑΜΑΤΑ ΡΕΥΣΤΩΝ ΚΑΙ ΕΞΙΣΩΣΗ BERNOULLI

Το υπέροχο με την επιστήμη και τα πειράματα είναι πώς μπορείς να απολαύσεις την χαρά που σου προσφέρει το παιχνίδι και δεν χρειάζεται να μεγαλώσεις ποτέ, ενώ ταυτόχρονα μπορείς να μαθαίνεις!

Πάμε να δούμε μέσα από κάποια πειράματα τα αποτελέσματα της εξίσωσης Bernoulli. Πριν περάσουμε στα πειράματα μας όμως να δούμε τι προκύπτει από την πασίγνωστη αυτή η σχέση.

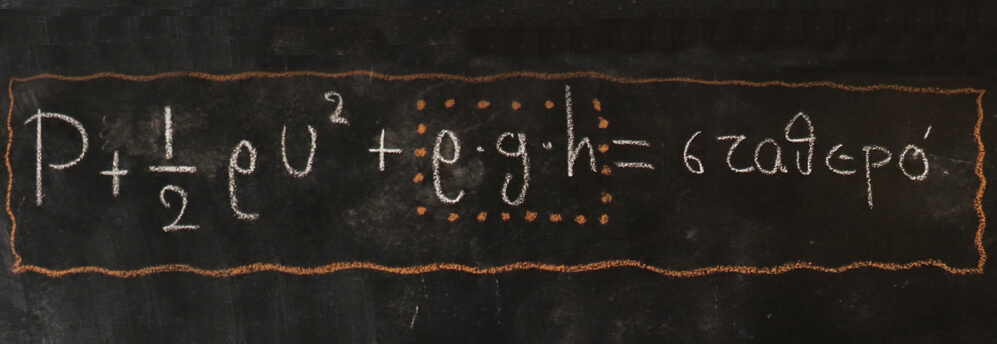
Σύμφωνα λοιπόν με αυτήν το βασικό συμπέρασμα είναι πως όσο η ταχύτητα αυξάνεται η πίεση που θα έχουμε θα μειώνεται. Αυτό προκύπτει από το γεγονός ότι παρατηρούμε πως το άθροισμα της πίεσης και της ταχύτητας μέσα σε αυτή τη σχέση θα πρέπει να παραμένει σταθερό. Άρα λοιπόν το βασικό συμπέρασμα πάνω στο οποίο θα βασιστούμε για την ερμηνεία των πειραμάτων μας είναι πώς: αυξάνει ταχύτητα μειώνεται η πίεση, μειώνεται η ταχύτητα αυξάνεται η πίεση.

ΠΕΙΡΑΜΑ ΜΕ ΚΟΥΤΑΚΙΑ ΑΝΑΨΥΚΤΙΚΟΥ

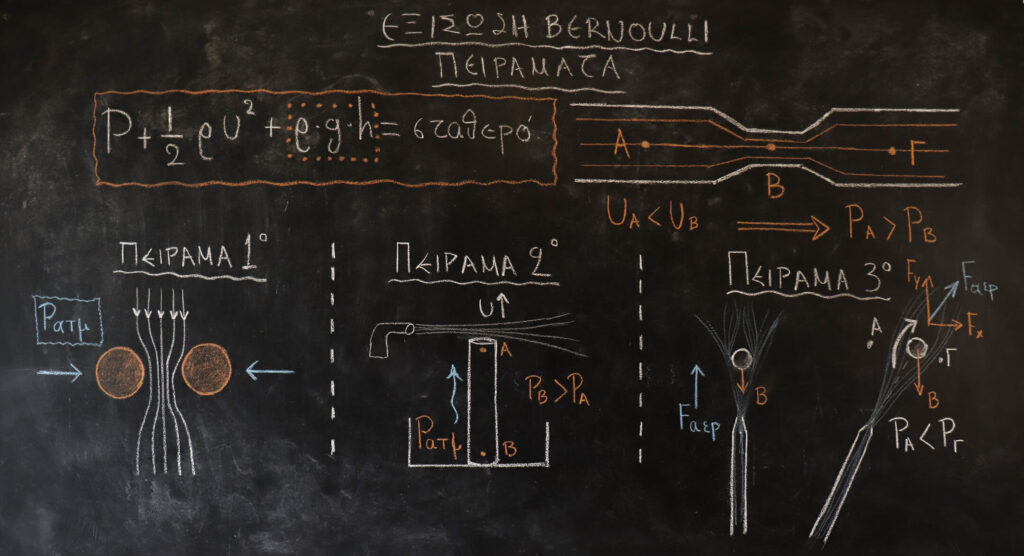
Έχοντας τα δύο κουτάκια τοποθετημένα πάνω στο τραπέζι και πριν φυσήξουμε, αυτό που θα περιμέναμε να συμβεί είναι ότι μόλις φυσήξω ο αέρας θα έπρεπε να εκτοπίσει τα κουτάκια με τρόπο που θα τα κάνει να απομακρυνθούν το ένα από το άλλο, όμως… Άυτό που παρατηρούμε αν το κοιτάξουμε σε κάτοψη όπως το έχω ζωγραφίσει είναι πως στο σημείο Β εξαιτίας της στένωσης που υπάρχει η ταχύτητα που κινείται ο αέρας αυξάνεται άρα η πίεση μειώνεται, κάνοντας έτσι την πίεση που υπάρχει στα σημεία Γ και Δ ,πού είναι η ατμοσφαιρική, να υπερισχύει έναντι της εσωτερικής πίεσης που υπάρχει στο σημείο Β ωθώντας έτσι τα κουτάκια να ακουμπήσουν το ένα το άλλο!

ΠΕΙΡΑΜΑ ΜΕ ΚΑΤΑΣΚΕΥΗ ΨΕΚΑΣΤΗΡΑ

Πριν φυσήξω στο επάνω μέρος του σωλήνα, τόσο στο επάνω μέρος όσο και στο κάτω μέρος του σωλήνα, η πίεση που έχουμε είναι η ατμοσφαιρική. Μόλις όμως φυσήξω στο πάνω μέρος έχουμε μία ταχύτητα που μεγαλώνει άρα η πίεση στο επάνω μέρος θα ξεκινήσει να μειώνεται. Συνεπώς η ατμοσφαιρική πίεση στο κάτω μέρος του σωλήνα θα είναι μεγαλύτερη, ωθώντας το υγρό να κινηθεί προς τα πάνω!

ΑΙΩΡΟΥΜΕΝΗ ΜΠΑΛΑ

Όταν αρχικά είχα την σωλήνα κατακόρυφη με φορά προς τα πάνω είναι λογικό να σκεφτεί κανείς πως η δύναμή του αέρα καθώς αυτή χτυπάει την μπάλα θα είναι ίση με την δύναμη του βάρους της μπάλας και ως αποτέλεσμα θα έχει να ισορροπήσει η μπάλα σε ένα σημείο. Και η σκέψη αυτή θα ήταν σωστή!  Το περίεργο όμως προκύπτει στην περίπτωση που στρέφουμε τον φυσητήρα υπό μία γωνία και αυτό που θα περίμενα αφού ο αέρας θα χτυπήσει την μπάλα υπό μία γωνιά είναι να την οδηγήσει στο να κάνει μία οριζόντια βολή πράγμα το οποίο δεν συνέβη! Στην περίπτωση λοιπόν αυτήν αυτό που προκαλέσαμε είναι και μία ταυτόχρονη περιστροφή της μπάλας. Αυτό σημαίνει ότι η ταχύτητα κατά την δεξιόστροφη φορά αυξάνει την ταχύτητα του αέρα στο επάνω μέρος της μιας και τον παρασέρνει στην ίδια φορά που αυτός έρχεται, ενώ σε αντίθεση από την κάτω μεριά που έρχεται ο αέρας έρχεται σε αντίθεση με την δεξιόστροφη περιστροφή της μπάλας κάνοντας έτσι τον αέρα από την κάτω μεριά να μειώνει την ταχύτητα του. Άρα λοιπόν αν μελετήσουμε μία ρευματική γραμμή στην επάνω μεριά η ταχύτητα του αέρα θα είναι μεγαλύτερη άρα και η πίεση στο σημείο που βρίσκεται από πάνω θα αρχίσει να μικραίνει. Αντιθέτως στην κάτω μεριά αν μελετήσουμε μία δυναμική γραμμή παρατηρούμε πως η ταχύτητα στο σημείο Γ θα είναι μικρότερη. Άρα αυτό σημαίνει πως η πίεση θα είναι μεγαλύτερη. Η διαφορά πίεσης αυτής που είναι από κάτω προς τα πάνω δημιουργεί μία δύναμη, την δυναμική άνωση, η οποία ωθεί την μπάλα προς τα πάνω κάνοντας την έτσι να ισορροπήσει!

Αυτά ήταν κάποια πειράματα που μας βοηθούν να κατανοήσουμε την υπέροχη εξίσωση του μπερνούλι και κάποιες εφαρμογές της μπορείτε και εσείς να κάνετε τα πειράματα αυτά στο σπίτι σας και για οποιοδήποτε απορία μπορείτε να μου γράψετε στα σχόλια!