
ΓΥΣΡΟΣΚΟΠΙΟ ΤΙ ΕΙΝΑΙ ΚΑΙ ΠΩΣ ΛΕΙΤΟΥΡΓΕΙ
Αν δεν έχετε δει ποτέ μέχρι τώρα τι είναι και τι μπορεί να κάνει ένα γυροσκόπιο, ετοιμαστείτε να μείνετε με το στόμα ανοιχτό! Με το πείραμα που θα παρουσιάσουμε θα νιώσουμε αρχικά ότι παραβιάζονται οι νόμοι της φυσικής αλλά αν μείνουμε μέχρι το τέλος θα δούμε πόσο αρμονικά θα δέσουν όλα.
Η ρόδα που χρησιμοποιήσαμε στο συγκεκριμένο πείραμα, η οποία αποτέλεσε το γυροσκόπιο μας, έκανε μία περιστροφική κίνηση γύρω από τον άξονά της, μιας και εμείς ήμασταν που της δώσαμε μία αρχική ταχύτητα προκειμένου να αρχίσει να περιστρέφεται. Για να κατανοήσουμε όμως αυτό το κατά κάποιον τρόπο σύνθετο πρόβλημα θα ξεκινήσουμε την αναφορά μας από την ευθύγραμμη κίνηση προκειμένου να εξοικειωθούμε με κάποιες έννοιες και να κατανοήσουμε αυτά που θα πούμε στο τέλος.
ΔΥΝΑΜΗ-ΤΑΧΥΤΗΤΑ-ΟΡΜΗ
Θέλω αρχικά να φανταστείτε ένα μπαλάκι του τένις το οποίο κινείται με μία ταχύτητα u προς τα δεξιά. Η ταχύτητα είναι ένα διανυσματικό μέγεθος, μας ενημερώνει δηλαδή για την κατεύθυνση που έχει το μέγεθος στο οποίο αναφερόμαστε. Στο παράδειγμα που ανέφερα με το μπαλάκι τέννις είπα πως κινείται προς τα δεξιά. Τώρα μπορούμε να ορίσουμε και την ορμή ενός σώματος που συμβολίζεται με το γράμμα P και είναι ίση με P = m*u. Εφόσον η ταχύτητα είναι διανυσματικό μέγεθος συμπεραίνουμε πως και η ορμή είναι διανυσματικό μέγεθος. Κατά την κίνηση του θέλω να σκεφτείτε ότι έρχομαι και ασκώ μία στιγμιαία δύναμη στο μπαλάκι , σαν ένα απαλό χτυπηματάκι, τότε αυτό θα αλλάξει λίγο την κατεύθυνση της κίνησης του και θα κινηθεί από δω και έπειτα για πάντα διαγώνια όπως φαίνεται στον πίνακα 1. Τώρα θέλω να σκεφτούμε πώς ασκούμε συνεχώς μία δύναμη f πάνω στο μπαλάκι του τένις η οποία θα είναι πάντοτε κάθετη στην ορμή. Άρα λοιπόν αν παρακολουθήσουμε την κίνηση που κάνει το μπαλάκι σιγά-σιγά σε slow motion θα δούμε πώς μοιάζει σαν η ορμή να κυνηγάει συνεχώς την δύναμη f. Και πάμε να περάσουμε λίγο στην περιστροφική κίνηση προκειμένου να γνωρίσουμε κάποιες έννοιες και εκεί.
ΠΕΡΙΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ-ΓΩΝΙΑΚΗ ΤΑΧΥΤΗΤΑ-ΣΤΡΟΦΟΡΜΗ-ΡΟΠΗ ΔΥΝΑΜΗΣ
Έστω λοιπόν ότι έχω ένα αντικείμενο, όπως είναι η ρόδα του ποδηλάτου. Η ρόδα αυτή έχει μία γωνιακή ταχύτητα που συμβολίζεται με το γράμμα ω. Ας υποθέσουμε ότι περιστρέφεται με φόρα αντίθετη από αυτήν του ρολογιού. Το θέμα είναι τώρα προς τα πού θα βρίσκεται το διάνυσμα της γωνιακής ταχύτητας; Στην περιστροφική κίνηση για να βρούμε το διάνυσμα της γωνιακής ταχύτητας θα χρειαστούμε έναν κανόνα, τον κανόνα του δεξιού χεριού. Σύμφωνα με αυτόν παίρνουμε το δεξί μας χέρι και προσανατολίζομαι τα τέσσερα δάχτυλα στην φορά περιστροφής της ρόδας, έπειτα τεντώνουμε τον αντίχειρα μας και αυτός μας δείχνει το διάνυσμα της γωνιακής ταχύτητας. Καλωσορίζουμε στο παιχνίδι και την ροπή δύναμης. Ροπή δύναμης ονομάζουμε το φυσικό μέγεθος που μας περιγράφει την ικανότητα που έχει μία δύναμη να περιστρέψει ένα σώμα. Η ροπή συμβολίζεται με το γράμμα τ και είναι ίση με τ=f*r . Για να καταλάβουμε καλύτερα την έννοια της ροπής θέλω να σκεφτούμε το εξής παράδειγμα. Έστω ότι βρίσκεστε μπροστά σε μία πόρτα και αυτό που θέλετε να κάνετε είναι να την ανοίξετε. Έστω λοιπόν ότι την πρώτη φορά ασκείται μία δύναμη 10Ν κοντά στον μεντεσέ δηλαδή κοντά στον άξονα περιστροφής και τη δεύτερη φορά ασκείται ακριβώς την ίδια δύναμη των 10 Ν στο πόμολο. Σε ποια περίπτωση θα ανοίξετε πιο εύκολα την πόρτα ; Η απάντηση φυσικά είναι πως η πόρτα θα ανοίξει πιο εύκολα όταν ασκήσουμε την ίδια δύναμη στο πόμολο. Γιατί; Διότι η ροπή είναι μεγαλύτερη. Και γιατί είναι μεγαλύτερη; Ο λόγος που είναι μεγαλύτερη αν κοιτάξουμε τον τύπο είναι το γεγονός ότι το r δηλαδή η απόσταση που άσκησα την δύναμη από τον άξονα περιστροφής είναι μεγαλύτερη όταν άσκησα την δύναμη στο πόμολο. Διότι το r ήταν πολύ μεγαλύτερο από ότι στην περίπτωση που άσκησα την δύναμη δίπλα από το μεντεσέ, δηλαδή δίπλα από τον άξονα περιστροφής. Πώς βρίσκουμε τώρα το διάνυσμα της ροπής; Το αντικείμενό μας, η ρόδα δηλαδή, περιστρέφεται γύρω από έναν άξονα , όπως βλέπουμε την ρόδα η οποία εμφανίζεται ζωγραφισμένη στον πίνακα . 1 Η ροπή θα βρίσκεται στον φορέα του άξονα περιστροφής, το θέμα είναι θα είναι προς τα πάνω ή προς τα κάτω; Και τσουπ!… Την απάντηση και πάλι έρχεται να μας την δώσει το δεξί μας χέρι. Κλείνω τα τέσσερα δάχτυλα με φορά που να δείχνουν τον τρόπο που η δύναμη θέλει να περιστρέψει το σώμα γύρω από τον άξονα περιστροφής και ο αντίχειρας μου δείχνει την φορά της ροπής. Και μπαίνουμε στην τελευταία εννοια πριν περάσουμε στο γυροσκόπιο. Στην έννοια της στροφορμής. Αν κάνουμε πάλι τον παραλληλισμό με την ευθύγραμμη κίνηση είχαμε πει πως η ορμή ενός αντικειμένου είναι ίση με το γινόμενο της μάζας επί την ταχύτητα. Οπότε κοιτάξτε πόσο λογικά θα εξάγουμε και τον τύπο της στροφορμής. Η στροφορμή συμβολίζεται με το γράμμα L, αντί για μάζα που είναι το μέτρο της αδράνειας ενός αντικειμένου θα βάλουμε το I που είναι η ροπή αδράνειας ενός αντικειμένου και αντί για u πού είναι η ταχύτητα θα βάλουμε ω που είναι η γωνιακή ταχύτητα. Συνεπώς ο τύπος είναι L=I*ω. Και η στροφορμή είναι ένα διανυσματικό μέγεθος και για να βρούμε προς τα πού θα είναι αυτό το διάνυσμα θα χρησιμοποιήσουμε για ακόμα μία φορά τον κανόνα του δεξιού χεριού. Διεύθυνση στον άξονα περιστροφής, τέσσερα δάχτυλα στην φορά περιστροφής και ο αντίχειρας μου δείχνει το διάνυσμα της ροπής της δύναμης. Και αισίως φτάνουμε πλέον στην επεξήγηση του γυροσκόπιο.
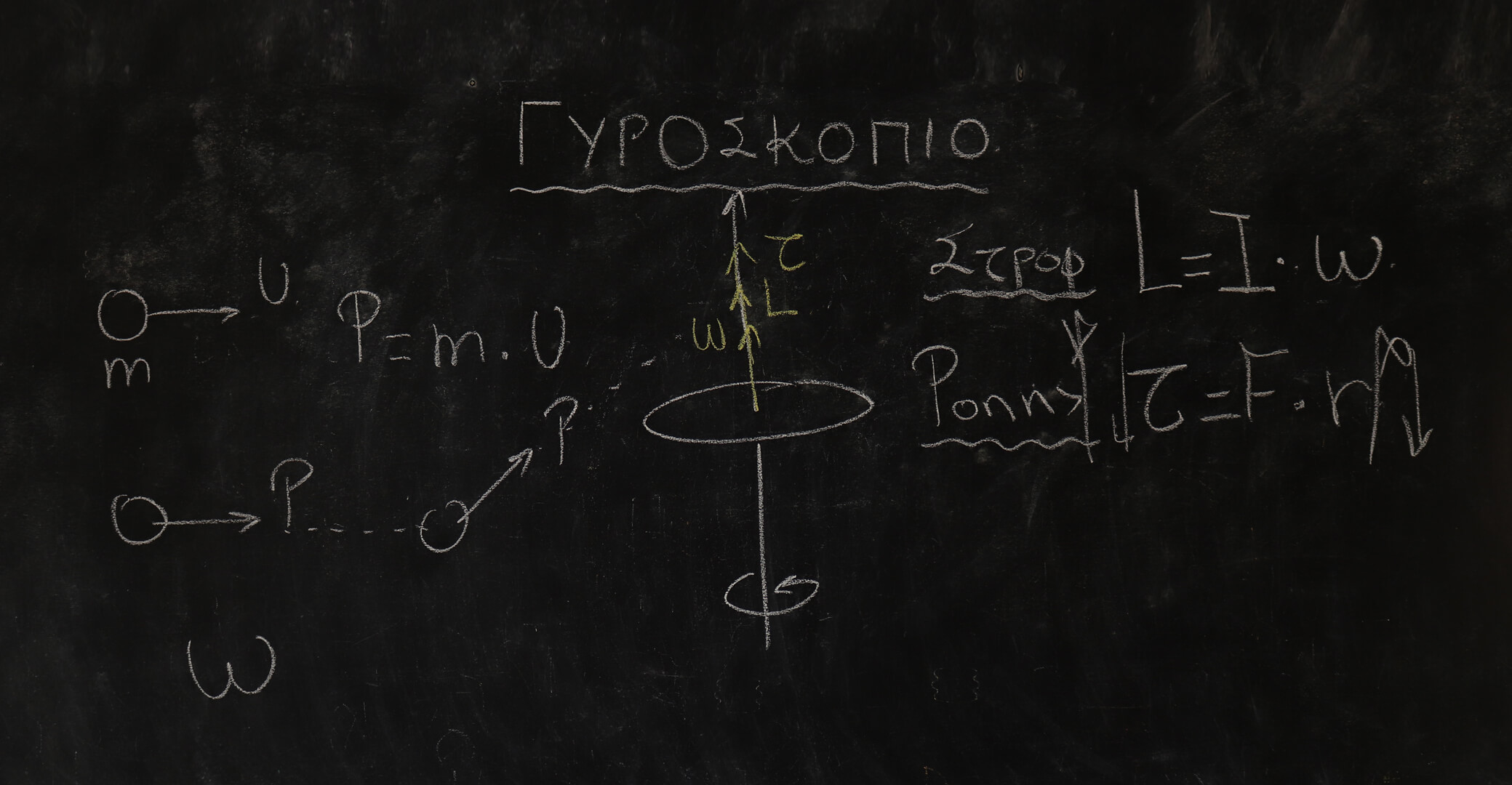
ΓΥΡΟΣΚΟΠΙΟ
Όταν η ρόδα μου ήταν ακίνητη και την άφηνα τότε αυτή απλά έπεφτε προς τα κάτω, και όλα έμοιαζαν λογικά και όμορφα. Το περίεργο ήταν πως όταν αυτή περιστρεφόταν με μία γωνιακή ταχύτητα δεν έπεφτε αλλά γυρνούσε γύρω από τον άξονά του σχοινιού. Αν κοιτάξουμε τον πίνακα 2 θα δούμε καλύτερα όσα θα αναφέρουμε. Τώρα ας θυμηθούμε λίγο το μπαλάκι του τένις. Το μπαλάκι του τένις είχε την ορμή και την δύναμη, ενώ εδώ στην περιστροφική κίνηση έχουμε αντίστοιχα την στροφορμή και τη ροπή δύναμης. Όπως είχαμε αναφέρει στο μπαλάκι του τένις η ορμή κυνηγούσε την δύναμη και κατά αυτό τον τρόπο ακολούθησε αυτή την καμπύλη πορεία. Αν λοιπόν σκεφτούμε με την ίδια λογική και την ίδια αναλογία στην περίπτωση του γυροσκοπίου η στροφορμή θα κυνηγάει την ροπή δύναμης και κατά αυτόν τον τρόπο η ρόδα μου περιστρέφεται γύρω από τον άξονά που σχηματίζει το σχοινί!
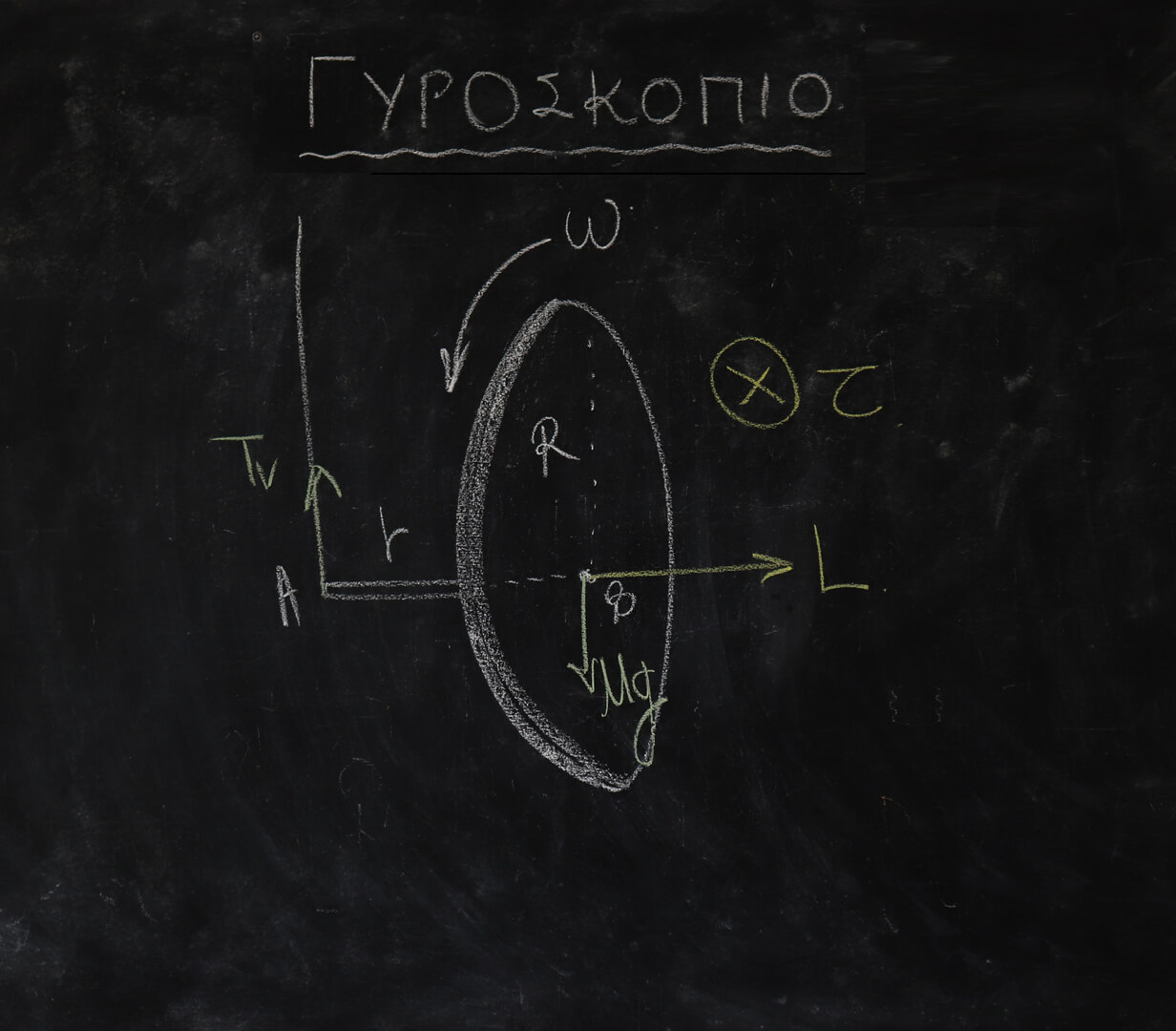
Tag:peirama


